This article on lines and angles is part of the elementary math that is asked in various competitive exams like SSC, banking, CLAT, etc. So it helps the students to get a basic understanding of the topic and makes them capable of solving the objective question based on this topic.

Fundamental terms of Lines and Angles

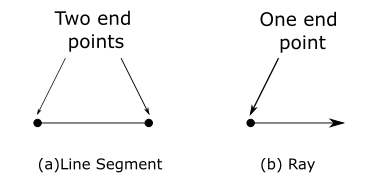
Line segment and Ray

A line segment is the part of a straight line whose both ends are fixed. If one point of a line is fixed then it is called as Ray.

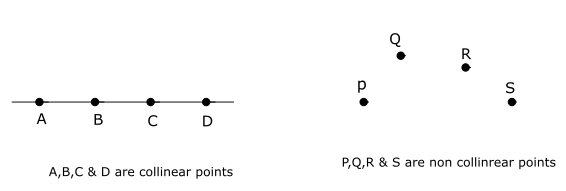
Collinear and Non-Collinear points

If three or more points line on a straight line then they are called collinear points. If three or more points do not lie on a straight line then they are called non-collinear points.

Types of angles

The types of angle are as follows:

Acute Angle: If an angle lies between 0° and 90°, it is called an acute angle.

Right Angle: An angle whose value is 90° is called a right angle.

Obtuse Angle: If an angle lies between 90° and 180° .it is called obtuse angle

Straight Angle: An angle whose value is 180 ° is called a straight angle.

Reflex Angle: An angle lies between 180 ° and 360 °, it is called a reflex angle.

Complementary angles

If the sum of two angles is equal to 90° then they mutually formed a set of complementary angles. The complementary angle of 40° is 50° and the complementary angle of 50° is 40°.

θ₁ + θ₂ = 90° ⇒ Set of Complementary Angles

Supplementary angles

If the addition of the two angles is 180° then they are said to be Supplementary to each other. The supplementary angle of 50° is 130° and the supplementary angle of 130° is 50°.

θ₁ + θ₂ = 180° ⇒ Set of Supplementary Angles

Adjacent Angles

Two angles are said to be adjacent angles if they have a common vertex, one common side, and their uncommon sides must be situated at 2 different sides of the common side.

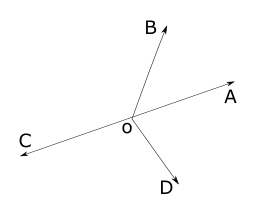
In the given fig 3

∠AOB and ∠COB are Adjacent angles because point O is common to both of them and their uncommon side OA and OC are opposite to the common side OB.

∠BOC and ∠DOC ; ∠AOD and ∠COD are Adjacent angles

But ∠AOB and ∠DOC; ∠BOC and ∠AOD are not adjacent angles as they do not have a common side.

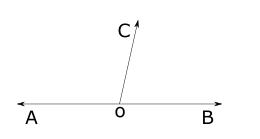
Linear Pair of angles

In the given figure 4. ∠AOC and ∠COB are adjacent angles and AOB is a straight line i.e, uncommon sides of adjacent angles form a straight line. Such angles are called linear pairs of angles.

Vertically opposite Angles

If Two straight lines AB and CD intersect each other at point O then the angle facing each other is called Vertically opposite angles.

In the given figure 5. ∠AOC and ∠DOB are one pair of Vertically opposite angles, while ∠AOD and ∠COB are another pair of Vertically opposite angles.

Transversal Line

A straight line that intersects two or more than two lines at distinct points is termed as a transversal line.

In the given fig 6. straight line a intersect two or more lines at b and c at point p and q, so a is a transversal line .

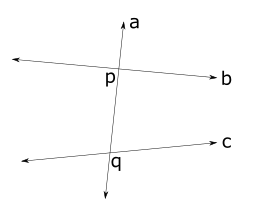
Exterior angle and interior angle

In the given fig 7, a transversal line intersects two straight lines b and c respectively at p and q. Around each point p and q, four angles are formed , among these angles ∠1 , ∠4, ∠7, ∠6 are called exterior angles while ∠2 , ∠3 , ∠5 , ∠8 are called interior angles.

Corresponding angles and alternate angles

In the fig 7 , the name of angles are as follows:

1. ∠1 and ∠5 ; ∠4 and ∠8 ; ∠2 and ∠6 ; ∠3 and ∠7 are called pair of corresponding angles.
2. ∠2 and ∠8 ; ∠3 and ∠5 are called pair of alternate interior angle.
3. ∠1 and ∠7 ; ∠4 and ∠6 are called alternate exterior angle.
4. ∠2 and ∠5 ; ∠3 and ∠8 are called consecutive interior angle.

The Exterior angle and Interior opposite angle of a triangle

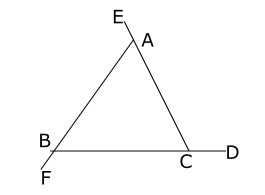
In the above fig 8,

∠A, ∠B, and ∠C are the interior angles of a triangle.

∠ACD, ∠CBF, and ∠BAE are the Exterior angles of a triangle.

Interior angles ∠A and ∠B are called interior opposite angles to the exterior angle ∠ACD

Interior angles ∠A and ∠C are called interior opposite angles to the exterior angle ∠CBF

Interior angles ∠B and ∠C are called interior opposite angles to the exterior angle ∠BAE

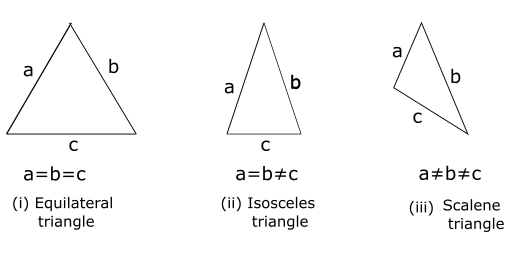
Types of Triangle according to size of sides:

Equilateral triangle: When the magnitude of all the three sides of a triangle is equal then the triangle is said to be an Equilateral triangle.

Isosceles triangle: When any two sides of a triangle are of equal magnitude then the triangle is said to be an isosceles triangle.

Scalene triangle: When all the three sides of a triangle are of different magnitude then the triangle is said to be a scalene triangle.

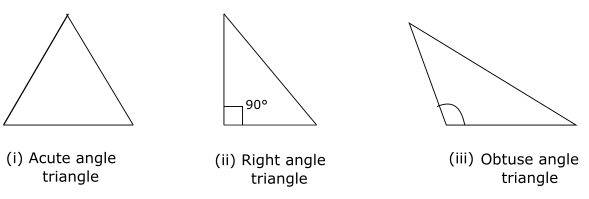
Types of triangles according to their angles

Acute angle triangle: If all the 3 angles of a triangle are acute then the triangle is said to be an acute angle triangle.

Right angle triangle: If one of the angles of a triangle is right angle i.e 90° then the triangle is said to be right angle triangle.

Obtuse angle triangle: If one of the angles of a triangle is obtuse i.e greater than 90° and less than 180 ° then the triangle is said to be an obtuse angle triangle. Any triangle can have only 1 obtuse angle.

Also Read : Theorem based on straight line & Angle and its fundamental terms