Important terms associated with Lines and Angles

This article on lines and angles is a part of the elementary math that is asked in various competitive exams like SSC, banking, CLAT, etc. So it helps the students to get a basic understanding of the topic and make them capable to solve the objective question based on this topic.

Fundamental terms of Line & Angle

Line segment and Ray

A line segment is the part of a straight line whose both ends are fixed. If one point of a line is fixed then it is called as Ray.

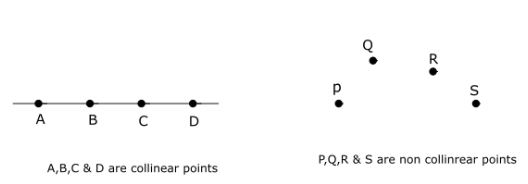
Collinear and Non-Collinear points

If three or more points line on a straight line then they are called collinear points. If three or more points do not lie on a straight line then they are called non-collinear points.

Types of angles

The types of angle are as follows:

Acute Angle: If an angle lies between 0° and 90°, it is called an acute angle.

Right Angle: An angle whose value is 90° is called a right angle.

Obtuse Angle: If an angle lies between 90° and 180° .it is called an obtuse angle

Straight Angle: An angle whose value is 180 ° is called a straight angle.

Reflex Angle: An angle lies between 180 ° and 360 °, it is called a reflex angle.

Complementary angles

If the sum of two angles is equal to 90° then they mutually formed a set of complementary angles. The complementary angle of 40° is 50° and the complementary angle of 50° is 40°.

θ₁ + θ₂ = 90° ⇒ Set of Complementary Angles

Supplementary angles

If the addition of the two angles is 180° then they are said to be Supplementary to each other. The supplementary angle of 50° is 130° and the supplementary angle of 130° is 50°.

θ₁ + θ₂ = 180° ⇒ Set of Supplementary Angles

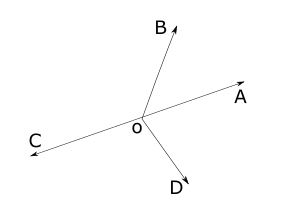
Adjacent Angles

Two angles are said to be adjacent angles if they have a common vertex, one common side, and their uncommon sides must be situated at 2 different sides of the common side.

In the given fig 3

∠AOB and ∠COB are Adjacent angles because point O is common to both of them and their uncommon side OA and OC are opposite to the common side OB.

∠BOC and ∠DOC ; ∠AOD and ∠COD are Adjacent angles

But ∠AOB and ∠DOC; ∠BOC and ∠AOD are not adjacent angles as they do not have a common side.

Linear Pair of angles

In the given figure 4. ∠AOC and ∠COB are adjacent angles and AOB is a straight line i.e, uncommon sides of adjacent angles form a straight line. Such angles are called linear pairs of angles.

Vertically opposite Angles

If Two straight lines AB and CD intersect each other at point O then the angle facing each other is called Vertically opposite angles.

In the given figure 5. ∠AOC and ∠DOB are one pair of Vertically opposite angles, while ∠AOD and ∠COB are another pair of Vertically opposite angles.

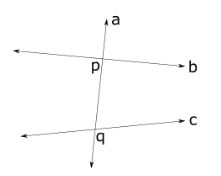
Transversal Line

A straight line that intersects two or more two lines at distinct points is termed as a transversal line.

In the given fig 6. Straight line a intersect two or more lines at b and c at point p and q, so a is a transversal line.

Exterior angle and interior angle

In the given fig 7, a transversal line intersects two straight lines b and c respectively at p and q. Around each point p and q, four angles are formed, among these angles ∠1 , ∠4, ∠7, ∠6 are called exterior angles while ∠2 , ∠3 , ∠5 , ∠8 are called interior angles.

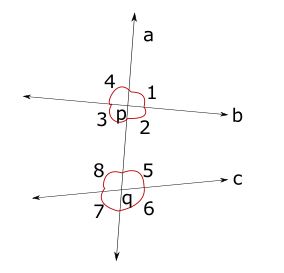
Corresponding angles and alternate angles

In fig 7 , the name of the angles are as follows:

1. ∠1 and ∠5 ; ∠4 and ∠8 ; ∠2 and ∠6 ; ∠3 and ∠7 are called pair of corresponding angles.
2. ∠2 and ∠8 ; ∠3 and ∠5 are called pair of alternate interior angle.
3. ∠1 and ∠7 ; ∠4 and ∠6 are called alternate exterior angle.
4. ∠2 and ∠5 ; ∠3 and ∠8 are called consecutive interior angle.

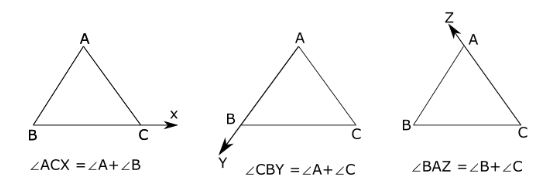
The Exterior angle and Interior opposite angle of a triangle

In the above fig 8,

∠A, ∠B, and ∠C are the interior angles of a triangle.

∠ACD, ∠CBF, and ∠BAE are the Exterior angles of a triangle.

Interior angles ∠A and ∠B are called interior opposite angles to the exterior angle ∠ACD

Interior angles ∠A and ∠C are called interior opposite angles to the exterior angle ∠CBF

Interior angles ∠B and ∠C are called interior opposite angles to the exterior angle ∠BAE

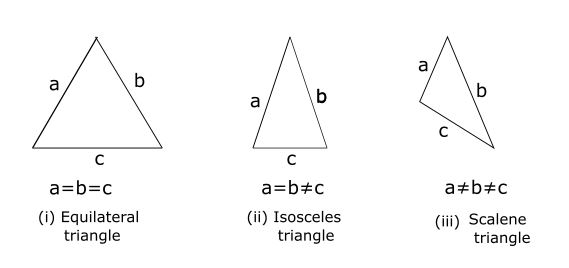
Types of Triangle according to the size of sides:

Equilateral triangle: When the magnitude of all the three sides of a triangle is equal then the triangle is said to be an Equilateral triangle.

Isosceles triangle: When any two sides of a triangle are of equal magnitude then the triangle is said to be an isosceles triangle.

Scalene triangle: When all the three sides of a triangle are of different magnitude then the triangle is said to be a scalene triangle.

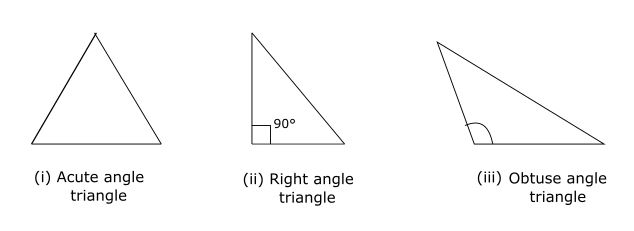
Types of triangles according to their angles

Acute angle triangle: If all the 3 angles of a triangle are acute then the triangle is said to be an acute angle triangle.

Right angle triangle: If one of the angles of a triangle is right angle i.e 90° then the triangle is said to be a right-angle triangle.

Obtuse angle triangle: If one of the angles of a triangle is obtuse i.e greater than 90° and less than 180 ° then the triangle is said to be an obtuse angle triangle. Any triangle can have only 1 obtuse angle.

Some important theorem based on angle and straight line

Theorem 1

If two straight lines intersect each other then the vertically opposite angles are equal.

∠AOB = ∠DOC (Vertically opposite angles)

∠AOD = ∠BOC (Vertically opposite angles)

Theorem 2

If a ray is incident on a line then the sum of the linear pair of angles thus formed is equal to 180° and its converse is also true.

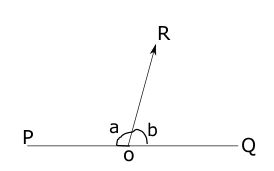
In the given figure 2, a ray R is incident on line PQ.
Therefore , ∠a +∠b = 180°
conversely, if ∠a +∠b = 180° then line POQ is a straight line

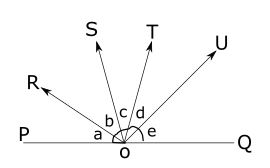
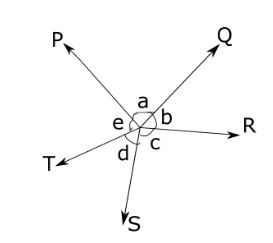
In general, if many rays are coming out of a single point O on the line then the sum of all linear pairs of angles is equal to 180°. So in the given figure 3, ∠a+∠b+∠c+∠d+∠e = 180°.

Theorem 3

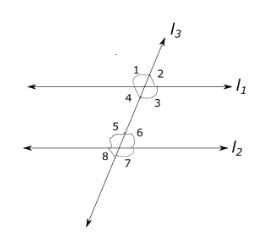
If Two parallel lines are intersected by a transversal line then the pair of corresponding angles thus formed are equal and its converse is also true .i.e if at least one pair of corresponding angles are equal then the two lines are parallel to each other.

In the given figure, two parallel lines l₁ and l₂ are intersected by a transversal line l₃. so the following pairs of corresponding angles are equal: ∠2=∠6; ∠1=∠5; ∠3=∠7; ∠4=∠8

Theorem 4

If two parallel lines are intersected by a transversal line, then the pairs of alternate angles are equal.

In fig 4,

∠3=∠5 and ∠4=∠6 (Alternate interior angles)

∠1=∠7 and ∠2=∠8 (Alternate exterior angles)

Theorem 5

Suppose two parallel lines l₁ and l₂ are cut by a transversal line l₃ then the addition of consecutive interior angles is equal to 180°. its converse is also true i.e if the addition of the consecutive interior angles between two lines l₁ and l₂ are equal to 180° then these two lines are parallel to each other. In the above fig 4,

∠3+ ∠6=180° and ∠4+∠5 = 180°

Theorem 6

In The given triangle △ABC, the sum of all three angles( ∠A, ∠B, ∠C ) is equal to 180°.

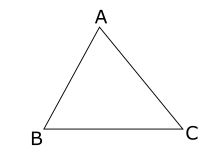
In the fig 5 , ∠A + ∠B + ∠C = 180°

Theorem 7

If any of the sides of a triangle △ABC is extended then the exterior angle so formed is equal to the addition of two interior opposite angles as shown below in fig 6.

Some Key points about Line and angles

1. When many lines originate from a single point then the Sum of all the angles around that point is 360°. In the given fig 7 . a+b+c+d+e = 360°

2. If the angle ∠ B and ∠ C of the given triangle is bisected by the line OB and OC respectively then

{\displaystyle \angle BOC\;=90^\circ\;+\frac{\angle A}2}

proof: In the given figure

3. (I) Addition of all the interior angles of a quadrilateral(4 sides) is 360°.

(ii) Addition of all the internal angles of a pentagon (5 sides ) is 540°.

(iii) Addition of all the internal angles of a Hexagon (6 sides ) is 720°.

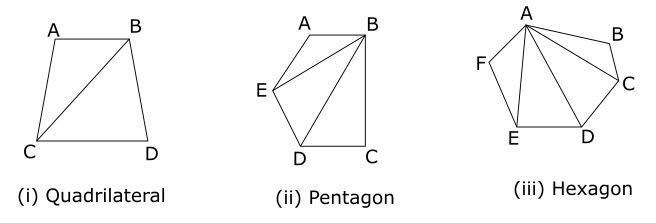
It is because of the fact that a quadrilateral can be divided into 2 triangles, a pentagon can be divided into 3 triangle, a hexagon can be divided into 4 triangles.

4. The sum of internal angles of an n-sided polygon is (n-2) x 180° .

Example – at n=4 sided polygon .i.e Quadrilateral internal angle is (n-2)x180° = (4-2)x 180° =360°

5. Each angle of n sided regular polygon (equal sides and angles) is {\displaystyle \frac{(n-2)180^\circ}n}

6. n sided polygon has {\displaystyle \frac{n(n-3)}2}

at n=4, Quadrilateral {\displaystyle \frac{n(n-3)}2=\frac{\displaystyle 4(4-3)}{\displaystyle 2}=2\;diagonals}

at n=5, pantagon {\displaystyle \frac{n(n-3)}2=\frac{\displaystyle 5(5-3)}{\displaystyle 2}=5\;diagonals}

at n=6, Hexagon {\displaystyle \frac{n(n-3)}2=\frac{\displaystyle 6(6-3)}{\displaystyle 2}=9\;diagonals}   etc.

Also Read : Important terms associated with Lines and Angles