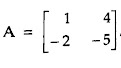This section of Control Systems Multiple Choice Questions and Answers (MCQs) focuses on “State-space analysis of control system”. These MCQs are very helpful for the preparation of University exams, Engineering exams, and various competitive exams.
CONTROL SYSTEM – STATE SPACE ANALYSIS MCQ’s
1. The State space analysis method is applicable to:
Explanation:- The advantage of the state-space analysis method is that it is applicable to Linear, Nonlinear, Time variant, Time invariant systems while conventional methods like Bode plot, Root locus, Polar plot, etc are only applicable to linear time-invariant(LTI) systems.
2. State-space analysis technique is a Frequency domain approach.
Explanation:- State-space analysis technique is a Time-domain approach.
3. The resolvant matrix ∅(s)is given by:
[sI-A]-1
L-1[sI-A]-1
L-1[sI-A]
Explanation:-The state transition matrix ∅(t) is the laplace inverse of resolvant matrix ∅(s) i.e ∅(t)= L-1∅(s) ,Also ∅(t) =L-1[sI-A]-1
4. A system is said to be ……….. if every state x can exactly be determined from the measurement of the output y over a finite interval of time.
Explanation:- Controllability: A system is said to be controllable if any initial state can be transferred to any final state in a finite time interval by some control input.
Observability: A system is said to be observable if every state can exactly be determined from the measurement of the output over a finite interval of time.
5. The eigen value of the matrix given below is
Explanation:- The eigenvalue can be calculated by using the characteristic equation |λI -A| =0 . so by saving this characteristic equation we get (λ+3)(λ+1)= 0.Hence eigenvalue, λ=-1 , -3.
6.For the state equation ẋ = Ax + Bu and y=Cx , the transfer matrix is :
-
C(sI-A)-1B
B(sI-A)-1A
A(sI-A)-1C
C(sI-A)-1A
-
ANSWER= (A) C(sI-A)-1B
Explanation:-The transfer matrix for the state equation is given as C(sI-A)-1B where A is the system matrix, B is the input matrix, and Cis output matrix.
7. Controllability of a system is checked by using the matrix:
- [B AB A2B …..]
[A AB A2B …..]
[C AC A2C …..]
Explanation:- The controllability of a system is checked by using controllable matrix QC = [B AB A2B …..] where A is system matrix and B is input matrix or control matrix.
8. Controllability of a system is checked by using the matrix:
- [CT : AT CT :
(AT)2CT …….. ]
[CT : AT (CT)2: (AT)2( CT)2 …….. ]
[CT: AT (CT)2 : AT (CT)3 …….. ]
D) None
Explanation:- The observability of a system is obtained by using observable matrix QO = [CT : AT CT : (AT)2CT …….. ]
where A is the system matrix and C is the output matrix.
9. The transfer can be decomposed to state equation or state diagram by which among the following methods:
Explanation:- The process by which transfer function changes to state diagram or state equations is called decomposition of the transfer function. The transfer function can be decomposed by three methods known as Direct decomposition, Cascade decomposition, and parallel decomposition.
10. The transfer function of a system is available only for the state which is:
Explanation:-The transfer function of a system is available only for the state which is both Controllable and Observable (SCO).
More Related MCQ’s