Table of Contents
Number System
A number is represented by (N)r , where r is the base and N is the number. A digital system uses the following types of number systems:
(I) Decimal number system, Example : (3286)10
(ii) Binary number system, Example : (1100111)2
(iii) Octal number system, Example : (4365)8
(iv) Hexadecimal number system, Example: (59AD)16
Decimal number system
A decimal number system has a base of 10 and it has 10 distinct symbols ( 0, 1, 2, 3, 4, 5, 6, 7, 8 & 9 ). By using these quantities we can express any quantity.
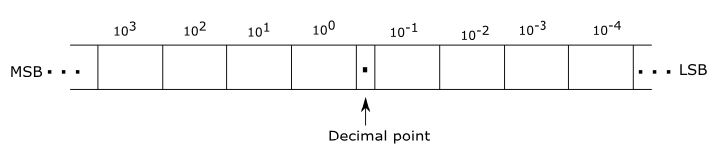
Example : Represent decimal number 89.27 in power of 10
N= 8 x 101 + 9 x 100 + 2 x 10-1 +7 x 10-2
The digit 8 has a weight of 10, the digit 9 has a weight of 1, the digit 2 has a weight of 1/10, and digit 7 has a weight of 1/100.
Binary Number System
The base of a binary number is 2 i.e. it has two base numbers 0 and 1. These base numbers are called bit . A group of 4 bits is termed as Nibble while the group of 8 bits is termed as Byte.

Example– Represent binary number 1101.101 in power of 2 and also find its decimal equivalent.
solution: The representation of given binary number 1101.101 in power of 2 is given below
N= 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 + 1 x 2-1 + 0 x 2-2 + 1 x 2-3
= 8 + 4 + 0 + 1 + 0.5 + 0 + 0.125
= ( 13.625 )10
so, ( 1101.101)2 = ( 13.625 )10
Octal Number system
This number system has a base of 8 and it possesses 8 distinct symbols i.e., 0, 1, 2, 3, 4, 5, 6, and 7. This system is very important in digital computing work.
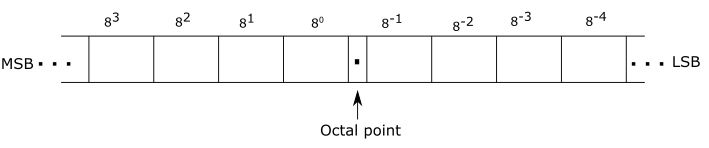
Example- Represent Octal number (206.4)8 in power of 8 and also find its decimal equivalent .
Solution : Representing given octal number in power of 8 as follows
N= 2 x 82 + 0 x 81 + 6 x 80 +4 x 8-1
= 128 + 0 + 6 + 0.5
=134.5
so , (206.4)8 = (134.5)10
Hexadecimal Number System
This number system has a base of 16 and it posses 16 different symbols for its representation (0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)
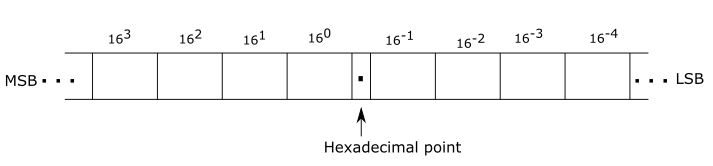
Example- Represent the Hexadecimal number (2CD.A)16 in the power of 16 and also find its decimal equivalent.
Solution: Representing the given Hexadecimal number in power of 16 is given as
N = 2 x 162 + 12 x 161 + 13 x 160 + 10 x 16-1
= 2 x 256 + 192 + 13 + 0.625
= 717.625
so, (2CD.A)16 = (717.625 )10
Number system conversion from one radix (base) to another radix (base)
Decimal number system to another base conversion
(I) Decimal to Binary Conversion
The decimal number is repeatedly divided by 2 and writing the remainder after each decision until a quotient of 0 is obtained.
Example: Convert (46.78)10 into its binary equivalent.
solution: Separating both integral and fractional parts of (46.78)10, we get (46)10 as an integral part and (.78)10 as a fractional part.

(ii) Decimal to octal Conversion
In this conversion process, the decimal number is repeatedly divided by 8 till the quotient becomes 0. This process is quite similar to decimal to binary conversion where the decimal number is repeatedly divided by 2 till the quotient becomes 0.
Example: Convert (532.6767)10 to octal.
Solution: Separating both integral and fractional parts of (532.6767)10, we get (532)10 as an integer part and (.6767)10 as a fraction part.

(iii) Decimal to Hexadecimal
To convert a decimal number into hexadecimal, the decimal number is repeatedly divided by 16 till the quotient becomes 0.
Example: Convert (8085.57)10 to its hexadecimal equivalent.
Solution: Separating both integral and fractional parts of (8085.57)10, we get ( 8085)10 as an integer part and (.57 )10 as a fraction part.

Binary number system to another base conversion
(i) Binary to decimal Conversion
In this conversion process, the binary number is multiplied by its positional weight, and then all the products are added together to get the equivalent decimal number
Example: convert a binary number (1010.11)2 to its decimal equivalent.
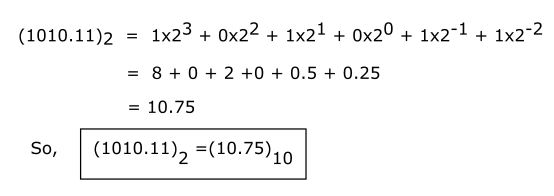
(ii) Binary to Octal conversion
In this conversion, the binary bitstream is grouped into pairs of three (starting from LSB ) and the Octal number is written for its equivalent binary group.
Example: Convert binary number (1100011111101.01101)2 to its Octal equivalent.

(iii) Binary to Hexadecimal Conversion
In this conversion, the binary bitstream is grouped into pairs of four bits (starting from LSB ) and a hexadecimal number is written for its equivalent binary group.
Example: Convert the binary number (1100011111101.01101)2 to its hexadecimal equivalent.

Octal Number system to another base conversion
(i) Octal to decimal conversion
An octal number can be converted to decimal by multiplying each octal digit by its position weight and all the products are added to get the equivalent decimal number.
Example: Convert (206.4)8 to decimal
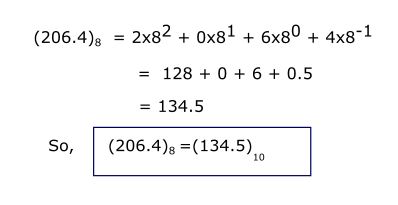
(ii) Octal to binary conversion.
This conversion can be done by converting each digit into a three-bit binary individually.
Example: Convert (274.5)8 into binary.
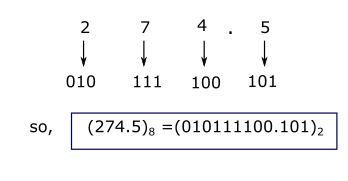
(iii) Octal to Hexadecimal
This octal to hexadecimal conversion process involves two steps, in the first step we have to convert octal into binary, and then in the second step binary will be converted into hexadecimal.
Example: Convert (472.5)8 into hexadecimal.
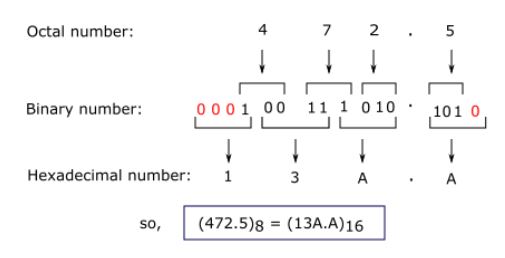
Hexadecimal number system to another base conversion.
(i) Hexadecimal to Decimal conversion
in this conversion each hexadecimal digit is multiplied by its weight and the products are added.
Example: Convert ( 2CD. A)16 to a Decimal number.

(ii) Hexadecimal to binary conversion
Base 16 is the fourth power of 2, hence representing each decimal digit by its 4-bit binary equivalent.
Example: Convert (B9D2. A)16 into a binary number.
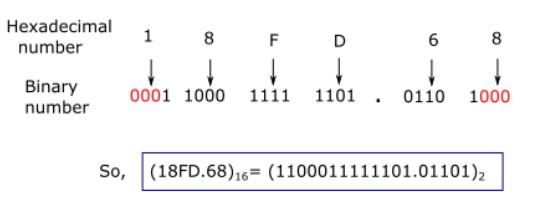
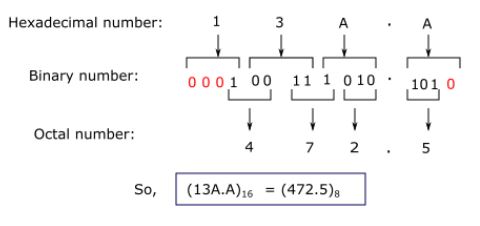
(iii) Hexadecimal to Octal conversion
This hexadecimal to octal conversion process involves two steps, in the first step we have to convert hexadecimal into binary, and then in the second step binary will be converted into octal
Example: Convert (13A.A)16 in.to octal number
.
Recommended Articles

